Standings Update

Compiled by Felix Perrone (WKU #76), here are all the current standings as of 12/18/2012:

The NCDA is working out how best to sort their standings, to help solve the problem of a spatially divided league without a set amount of games per team. Check out a detailed description of all the standings after the jump…

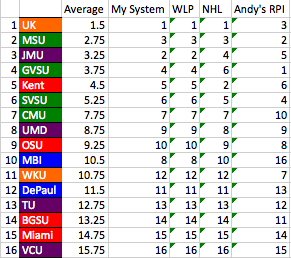
• Column A denotes the standing place.
• Column B denotes the team and region by color.
• Column C is the average of all the other rankings.
• Column D is the Perrone System
• Column E is basic Win/Loss Percentage
• Column F is the current NHL style
• Column G is the Lieblich System

Column D: The Perrone System:

A win against a team with a 1.0 WLP (win-loss percentage) equals 4 points
A win against a team with a WLP of .75-.999 = 3.5 points
A win against a team with a WLP of .5-.749 = 3.25 points
A win against a team with a WLP of .25-.499 = 3 points
A win against a team with a WLP of .001-.249 = 2.75 points
A win against a team with a WLP of 0 = 2.5 points

Then you add:

An OT-L (Overtime Loss) against a team with a 1.0 WLP = 1.05 points
An OT-L against a team with a WLP of .75-.999 = .975 points
An OT-L against a team with a WLP of .5-.749 = .95 points
An OT-L against a team with a WLP of .25-.499 = .925 points
An OT-L against a team with a WLP of .001-.249 = .9 points
An OT-L against a team with a WLP of 0 = .875 points

Then from that total number you get, you subtract the losses:

A loss against a team with a WLP of 1 = -1.25 points
A loss against a team with a WLP of .75-.999 = -1.375 points
A loss against a team with a WLP of .5-.749 = -1.5 points
A loss against a team with a WLP of .25-.499 = -1.625 points
A loss against a team with a WLP of .001-.249 = -1.75 points
A loss against a team with a WLP of 0 = -2 points

Then you divide all that by TGP (Total Games Played)

So the very basic formula is:

((Wins+OT-Ls)-(Losses))/TGP

But within those Wins, OT-Ls, and Losses would be the wins against teams with WLP of 1, >.75 but <.999, etc

Felix’s top five is:

1. UK
2. JMU
3. MSU
4. GVSU
5. Kent

Column E: Win/Loss Percentage:

Simply games won over games lost. Overtime does not affect the outcome.

1. UK
2. JMU
3. MSU
4. GVSU
5. Kent

Column F: NHL-style Standings:

Used for Nationals 2012, and by default the 2013 season, the breakdown is actually sorted first by most Points (W=2, OTL=1, L=0), then highest W/L%, then most matches, and lastly by date of entry into the NCDA.

1. UK
2. Kent
3. MSU
4. JMU
5. SVSU

Column G: RPI – The Lieblich System:

Lastly. the RPI rankings have been developed by Andy Lieblich (MSU #20). It works like this: “It’s your team’s win percentage x .25+ your opponent’s win percentage x .50+ your opponent’s opponent’s win percentage x .25. This makes strength of schedule a bonus, so not only is winning important but beating good teams is beneficial.”

The top five for the RPI rankings are:

1. GVSU
2. MSU
3. UK
4. SVSU
5. JMU